3. 線形解析と非線形解析の違い
設計者CAEは線形解析から始めるのが一般的ですが、それは解析の基礎式が材料力学の理論からできているからです。しかし世の中の事象の多くは線形ではなく非線形で表現されるため、設計者CAEにおいてもよりリアルなシミュレーションが求められることが多くなり、非線形解析のニーズが高まりつつあります。非線形解析は、非線形性のタイプから大きく以下の3つに分類できます。
- 幾何学的非線形(大変形)
- 材料非線形(弾塑性、超弾性・・・)
- 接触(有限すべり、摩擦・・・)
ではお馴染みの「分布荷重が作用する両端支持ばり」を例にとって線形解析と幾何学的非線形解析による計算結果を比較してみます。
まず図1のように、幾何学的非線形解析では応力が上下面で対称ではなくなります。これは中立面に膜応力が発生するためです。離れた2点間に張られた糸の中点を指で押さえてたわみを与えると糸はピンと張って張力が発生してたわみがあまり増大しません。この張力がはりの場合は膜応力として発生します。膜応力は有限のたわみが存在して初めてそれを分力とした力のつりあい式にて計算できます。
このように幾何学的非線形では荷重が増えると膜応力も増えるため最大応力は非線形的に増加します。
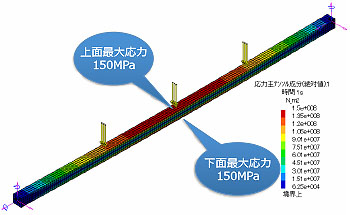
線形解析
- 上下面対称の曲げ応力のみ発生する
- 材料力学の公式と同じ計算結果になる
- 荷重の大きさと最大応力は線形の関係あり
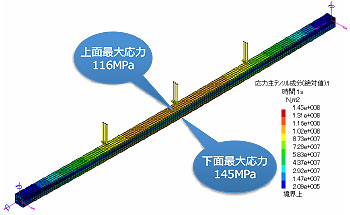
幾何学的非線形解析
- 曲げ応力と膜応力が発生する
- 材料力学の公式では計算できない
- 荷重の大きさと最大応力は非線形の
関係になる
図1. 線形解析と幾何学的非線形解析の応力結果比較
また図2のように、幾何学的非線形解析のときの最大たわみは膜応力の発生によりたわみが抑えられて線形解析のときより小さくなります。
線形解析は微小変形理論(すなわち変形が限りなくゼロに近い状態での力のつりあい)に基づいているため張力は計算されず、曲げ応力だけを計算するので荷重が増えると最大応力も線形的に増加します。
従来通りの標準や規格に則った製品設計では安全サイドで設計するのが基本になるので、まずは線形解析による設計者CAEを取り入れて設計検討の自由度を広げてより良い製品を開発するのが先決と考えます。
線形解析
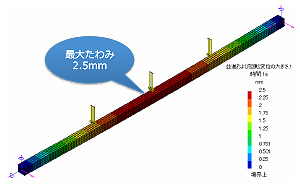
幾何学的非線形解析
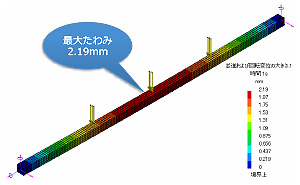
図2. 線形解析と幾何学的非線形解析の変位結果の比較
次に最適化を追求した設計では非線形解析を用いたリアリスティック・シミュレーションを取り入れていく必要があります。その簡単な例をご紹介します。
図3のようなバックルのクリップを設計するときに、従来通りの線形解析で応力を計算して許容応力以下になるように安全サイドに設計すると、強度的には満足するものになります。しかし剛性を必要以上に強くすると、クリップを押し込むのに予想以上の大きな力が必要になって逆に使い勝手が悪くなります。度を越すと消費者に見放されることにもなりかねません。
幾何学的非線形を考慮した計算は線形解析と同様にほとんど手間をかけずに容易に行えます。さらに材料非線形性の考慮を追加するとより現実に近いシミュレーションができるので、耐久性に優れて、かつ使い勝手の良いバランスの優れた製品を設計できることになります。
この例のように現実の事象を模擬した解析を行うには非線形性の考慮が望ましいことが分かります。
- 最大応力:非線形解析 < 線形解析
- 押込み力:非線形解析 < 線形解析
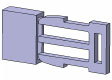
幾何学的非線形解析の場合
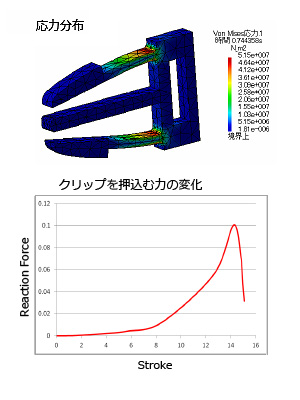
線形解析の場合
図3. バックル・クリップの最適設計に対する適用効果
CATIA V5のANLおよびATHは設計者が容易に使える非線形解析ツールです。設計者CAEでの非線形解析について関心をお持ちの方はぜひ弊社へお問合せください。
さて次号では、線形解析の話題に戻って「フォン・ミーゼス応力の真意」についてお話しする予定です。
以上
2013年 3月
※このサイトに掲載のイラスト・写真・文章の無断転載を禁じます。すべての著作権は株式会社ファソテックに帰属します。