フォン・ミーゼス応力の真意

CATIA GPSを使って設計者CAEに取り組みはじめると、最初の一歩で「Von Mises応力」に出会います。しかし「Von Mises応力」は学生時代に材料力学を学んだ人以外にとっては耳慣れないものであり、一体どのような応力なのか尋ねたくなる人が多いかと思います。そこで今回はこの「Von Mises応力」についてその意味と使い方をご紹介します。

まず「Von Mises応力」はフォン・ミーゼス応力と発音します。フォン・ミーゼスは人の名前で1900年代に力学分野で活躍された中欧出身の科学者です。さて、フォン・ミーゼス応力に言及する前に、材料の特性の一つである応力～ひずみの関係について簡単に触れます。応力とひずみの関係は材料の種類ごとに異なる応力～ひずみ曲線で表されます（図1サンプル参照）。

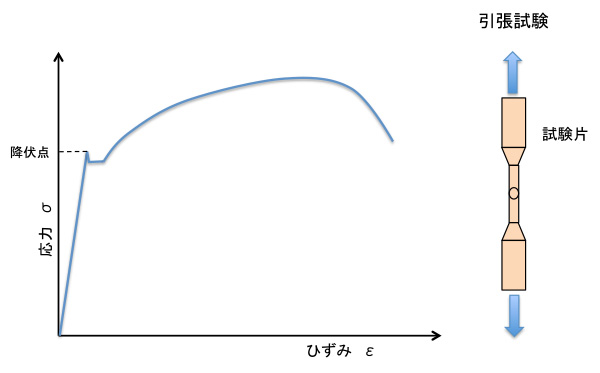
図1. 金属材料の応力～ひずみ曲線

この曲線は細長い試験片に単軸の引張荷重をかけて測定した荷重方向の応力とひずみの値をプロットして得られます。金属材料の応力～ひずみ曲線をみると降伏点と呼ばれる屈折点が見られます。この降伏点以下の応力状態では弾性変形が生じても除荷すると元の形状に戻ります。しかし降伏点を越えると材料は永久変形が始まります。これを塑性変形と呼びます。
設計者CAEの世界では製品が使用状況下で永久変形を生じないように設計するのが一般的ですので、CAEで計算された応力が降伏点より十分小さな値（実際は安全率を考慮した許容応力）以下になるよう設計します。

単軸の荷重下の場合であれば計算した発生応力を降伏点と照合して弾性範囲内であるか容易に判別できますが、荷重が2軸や3軸の複雑な環境下では応力成分が複数になりどの成分と降伏点応力を比較すべきか迷うことになります。このような多軸の荷重下の場合は、ある理論に基づいてスカラー値で表現した相当応力を降伏点応力と比較し弾性範囲内かどうかを判別します。
この背景になる理論はいくつかありますが、フォン・ミーゼスはせん断ひずみエネルギー説に基づく相当応力による降伏条件を提唱しました。よって、その相当応力のことをフォン・ミーゼス応力と呼ばれています。フォン・ミーゼス応力はスカラー値で大きさは絶対値で表し、方向を持っていません。3軸の主応力空間でせん断ひずみエネルギー説を図示すると図2に示す円柱で表されます。ここで円柱の内側は弾性状態、円柱面が弾性破損基準となります。

3軸主応力空間における
せん断ひずみエネルギー説降伏曲面

3軸主応力空間におけるせん断ひずみエネルギー説降伏曲面

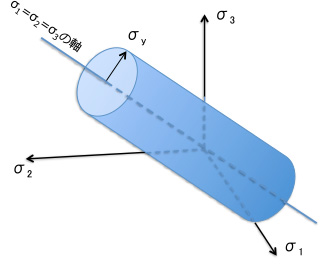
ここで、σ₁,σ₂,σ₃は主応力、σyは降伏点応力

2軸主応力平面（σ₂=0）における
せん断ひずみエネルギー説降伏曲線

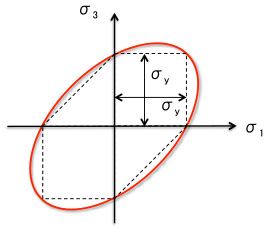
図2. せん断ひずみエネルギー説の降伏条件

すなわち、3軸の主応力値が円柱面上に位置すると降伏開始していることになります。フォン・ミーゼスが唱えたせん断ひずみエネルギー説は、金属などの延性材料の特性によく合うので一般的に広く用いられており、CATIA GPSでは計算結果の応力分布を表示するときに「Von Mises応力コンター」がデフォルトになっています。以上のようにフォン・ミーゼス応力は設計者CAEにおいて、製品の許容応力と照合して強度が十分であるかどうかを判断する重要な指標になります。

なお降伏条件としてよく知られているものには、他にTresca(トレスカ)が提唱した最大せん断応力説や脆性材料の特性に合う最大主応力説があります。応力および降伏条件についてもっと詳しく知りたい方は、弊社の教育コースの受講をお勧めします。

次回は「特異点に気を付けよう」と題して、設計者が陥りやすい応力分布の着目ミスについてご紹介します。