5. 特異点に気を付けよう
設計者CAEを始めたばかりの初心者の多くは、解析結果を評価するときにフォン・ミーゼス応力のカラーコンターを表示して、一番赤く染まった最大値が出ている箇所に着目します。この着目の仕方は時々適切でない場合がありますので注意が必要です。
弾性解析の場合、集中荷重が作用する点や集中応力が発生する点の応力は正しく計算されないので、応力特異点と呼ばれています。この特異点が存在する解析モデルでは特異点に最大応力が発生してしまうことが多いので、最大値のみに捕われると誤った評価を引き起こします。さらにその計算された応力値は正しい値ではありませんので、この値を評価することは避けなければなりません。なぜなら弾性解析の場合、特異点応力の理論値は無限大になるからです。
∵ 計算式を簡略化して表すと、応力 = 荷重値 ÷ 面積ゼロ = ∞
では解析モデルに特異点が存在するかどうかの判断が必要になりますので、特異点の見つけ方の一例をお話します。
図1に示すサンプルモデルでは形状から見て切り欠き部に応力集中が起こるので、特異点の存在が想定されます。CAEのベテランはすぐに分かりますが、初心者の方は気が付かないことが多いと思います。

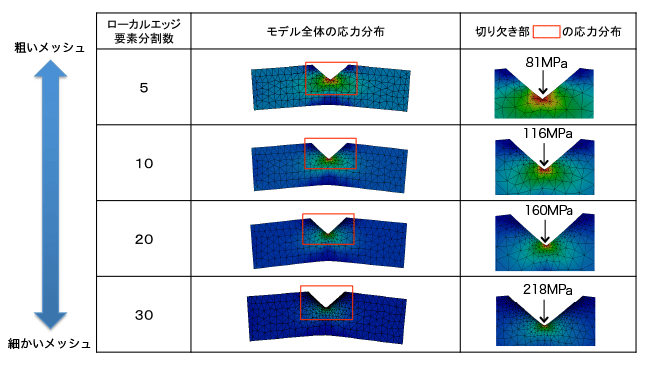
図1. 特異点のあるモデルの最大応力値変化
このようなモデルについては、徐々にメッシュ分割を細かくして計算を繰り返すと特異点の応力がどんどん大きくなり、収束することがありません。図3に応力の漸増する様子を青線で示しますが、メッシュを細かくするにつれて最大応力が増々大きくなっています。このように計算精度を上げるためにメッシュを細かくしていって応力がいつまでも収束しない点があれば、それは応力の特異点ということになります。
このような特異点が存在するモデルでは特異点周辺を評価対象から外して応力の分布を見るべきです。
一方、図2に示すようにサンプルモデルの特異点周辺にフィレットを施した形状に変更すると、応力集中は緩和されてメッシュ分割を細かくしていくと応力がある値に収束しています。図3に応力が収束する様子を赤線で示します。この形状のモデルは特異点が存在しなくなるので最大応力値で評価できます。また、メッシュを細かくしていくと応力値が収束しているので、得られた応力結果も良好な精度があり、評価に供することができます。

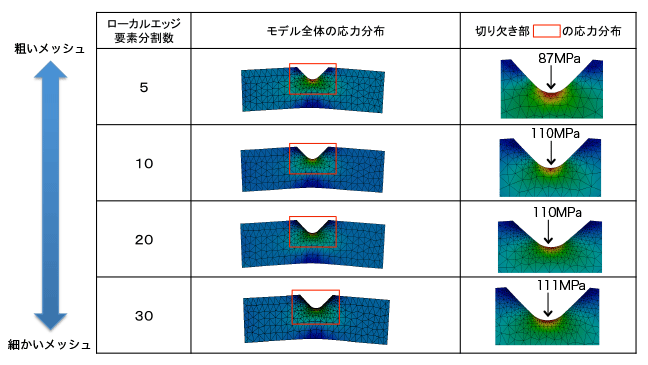
図2. 特異点のないモデルの最大応力値変化
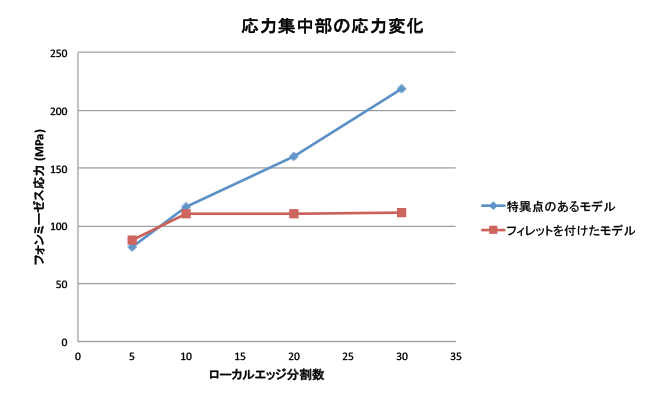
図3. メッシュ分割数に対する特異点応力の変化
応力の特異点は上記の形状のほかに、固定拘束面の境界線やL型形状の屈折点等にも存在します。
特異点への対応についてさらにお知りになりたい方は、弊社開催のCAE教育コース「設計者のための有限要素法」の受講をお勧めします。
次回は「計算結果の精度を保つメッシュサイズの目安」についてお話します。
以上
2013年 5月
※このサイトに掲載のイラスト・写真・文章の無断転載を禁じます。すべての著作権は株式会社ファソテックに帰属します。